
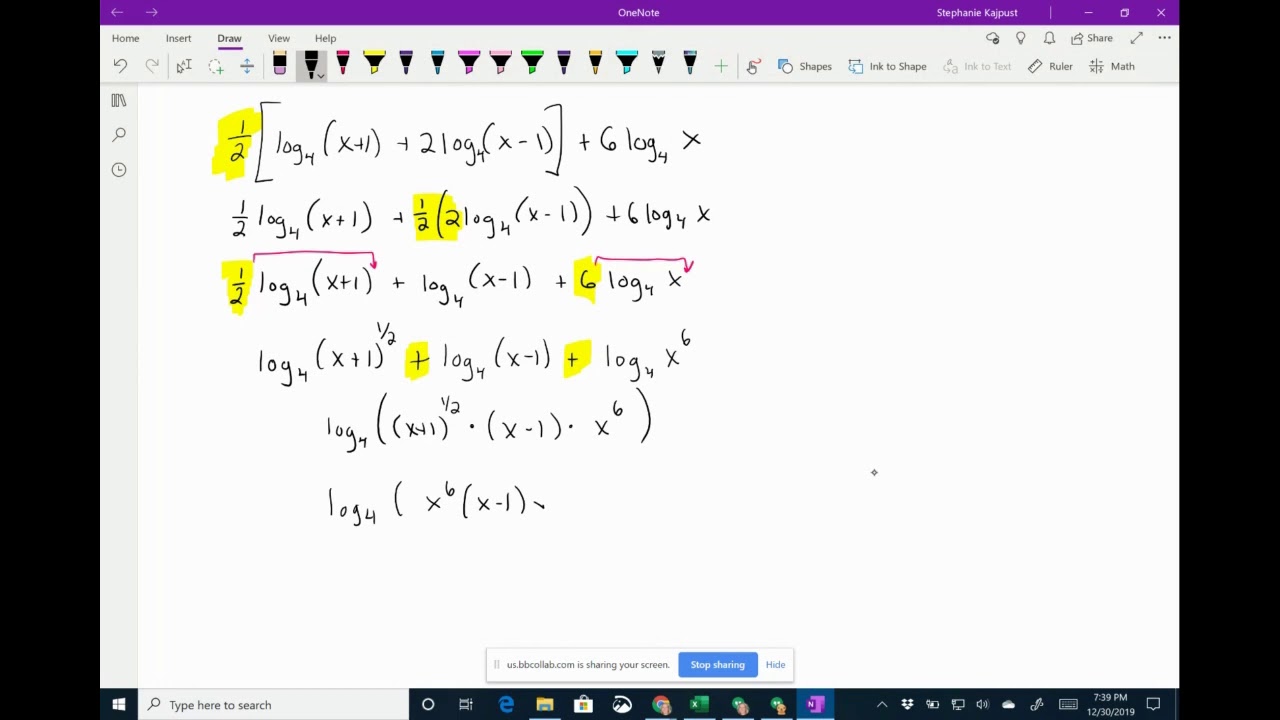
#Condense log full#
Additionally, I think I agree with other posts regarding the sweetness factor of the full can of SCM.

It gives the vanilla pudding a banana flavor that isn’t quite the same with the boxed, banana-flavored pudding mixes. I have often added a mashed banana (or more to taste), just after I mix the pudding and milk, and then add the sweetened condensed milk. Having said that, I will offer a variation that my family and friends seem to like. The 5 stars are for THIS EXACT recipe (well, with the exception of the 14 banana's - wow, must be a misprint, right? – I used 5). This is a very good "quick and easy" Banana Pudding recipe, when there's little time for either Cook & Serve, or, better yet, a truly homemade pudding recipe. Scroll through to find our best baked chicken wing recipes of all time, including baked Buffalo wings, baked teriyaki wings, baked BBQ wings, baked lemon pepper wings, and more. And you don't even need any fancy appliances to cook them because all these recipes are made in the oven for extra crispy wings that are packed with finger-licking-good flavor. Plus, how many foods come with their own convenient built-in handle? When it comes to flavors, the mighty chicken wing has something for everyone, so whether you like them spicy, cheesy, or a little bit sweet, you'll find a recipe that's just right for you on Allrecipes. Whether you're serving them as a snack at a party, an appetizer before dinner, or dinner itself, no one is able to resist this delectable finger food.
#Condense log plus#
So we're going to get 3 lin x, plus lin y minus a half, then w minus 2, then and then we've gone from having 1 log to having 1234 ser your question.Our 15 Best Baked Chicken Wing Recipes of All Time Are Why Napkins Were Invented Chicken wings are a real crowd-pleaser. Lin of e is simply 1 and then we're going to use the first rule we talked about so the powers inside become multiplication outside.
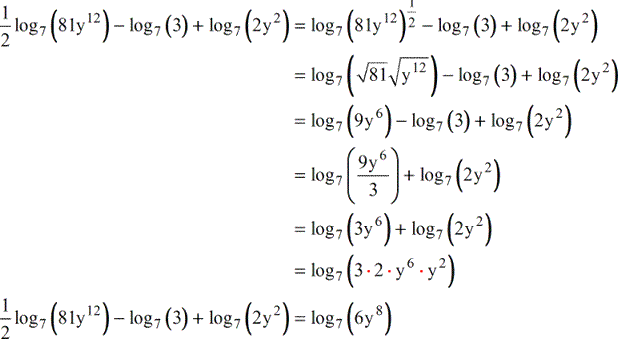

So doing it term by term we'll get line plus lin of x, cubed, plus lin of y minus lin, all the square root of that's w to the power of a half minus lin of z, squared and so looking at this first term. Now, looking at this 1 over here, we're wanting to do the opposite, so we're going to do exactly the same process we did here, but in reverse so first we're going to turn our multiplication and division inside the log into additional subtraction outside the log. So we've got x, squared y to the power of 6, divided by z, to the power of a half. So addition outside becomes multiplication, division outside becomes sorry, subtraction outside becomes division, and this is going to rouse to combine all of this into a single log. So this is going to give us the log of x, squared plus log of y to the power of 6, because we've got 2 multiplied by 3 out here: minus log, o z to the power of a half and then we're going to apply our second rule. So this is our powers inside logs become multiples outside of logs, and the second rule that we need to remember is that log of a plus log of b is equal to log of a times b, so multiples inside logs become additions outside of logs, and so Now we're ready to solve these 2 equations here so first we're going to apply the first rule, so the multiples become powers. In fact, so, let's call it x is going to be equal to the same log of a to the power of x. The first 1 that we want to remember is that log of a multiplied by 2 or any number right here. Okay, so to solve these 2 questions here, we want to remember our kind of 2 important rules of logs.


 0 kommentar(er)
0 kommentar(er)
